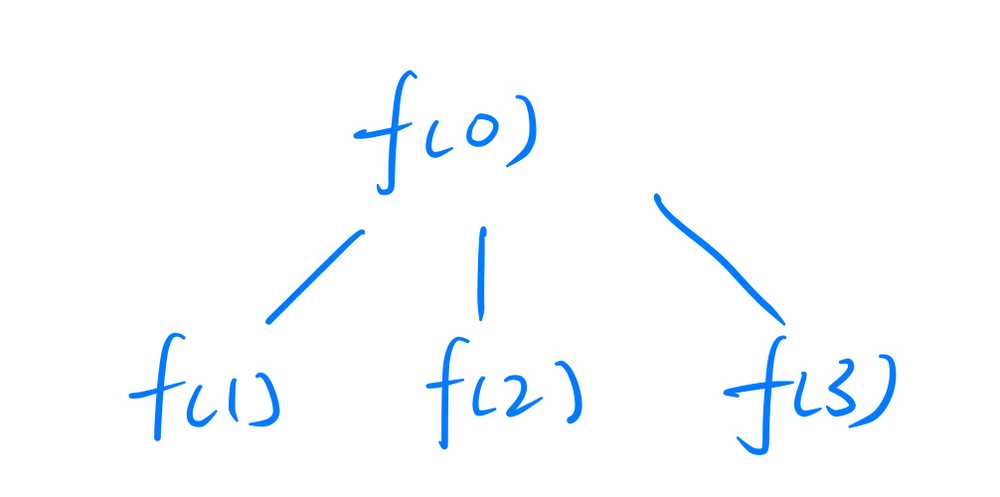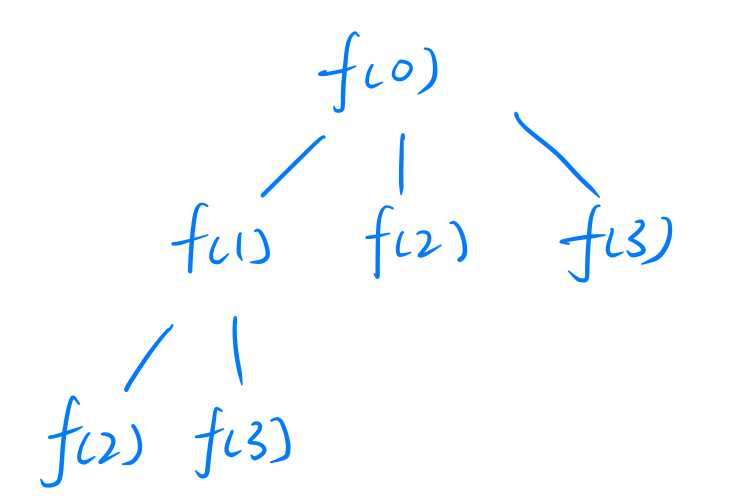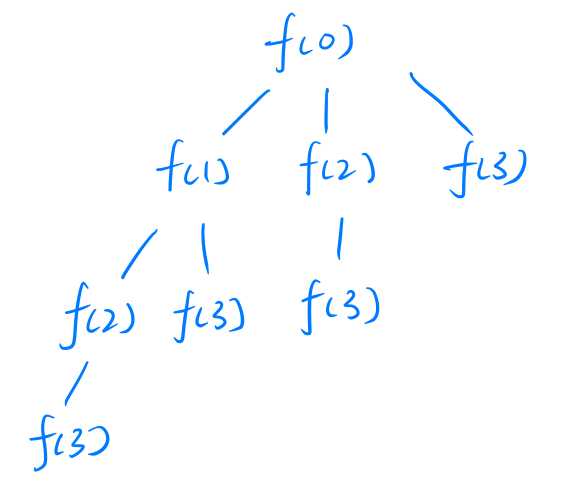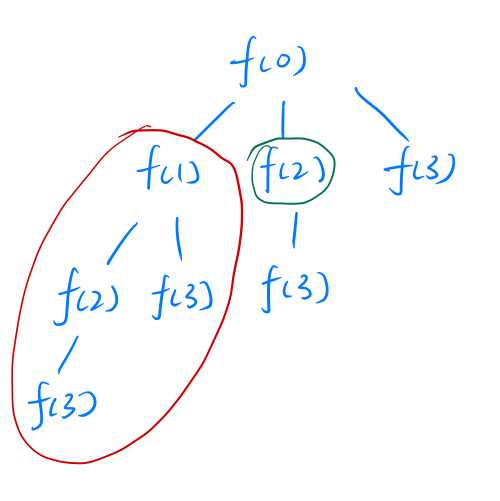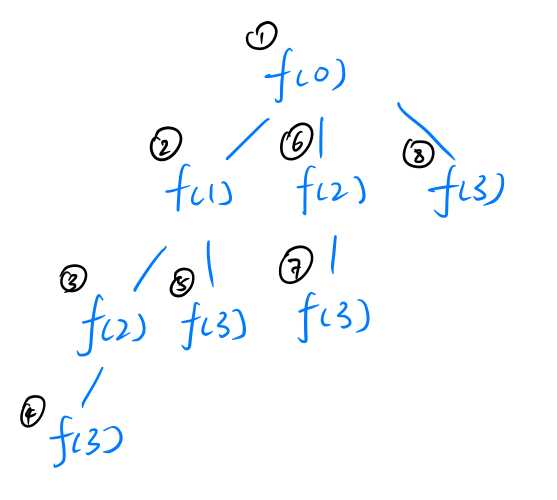Understanding Loops in Recursive Functions

February 15, 2019

Recently my friend asked me one question regarding how to interpret the loops in the recursive functions. At first I thought it was fairly easy to understand. Until I dive into the problem, I found it was actually quite challenging in understanding the order of function executions. Today, let me summarise my thoughts about this problem.

Jump to the conclusion if you would like to skip the analysis and directly hear my advise.

Problem Description

It’s a very short piece of Java code.

Class Playground {
    public static void main(String[] args) {
        printNum(0);
    }

    public static void printNum(int num) {
        for(int i = num; i < 3; i++) {
            System.out.println(num);
            printNum(i + 1);
        }
    }
}

printNum() functions are recursively called in a for loop within the function and it loops 3 times.

In the end, it prints

Now here is the problem, how does the program executed?

Analyse the Problem

1st Level

Apparently, in the main() function, printNum() is only called once. So we may consider it as a parent node of all the recursive functions, denoted as f(0), where f() refers to printNum(). This is the 1st level.

In the for loop of f(0), f() is called 3 times with value passed in as 1, 2 and 3 respectively.

That is because for(int i = num; i < 3; i++) indicates that the loop starts from i = 0 to i = 2, and the recursive function takes i + 1 as parameters.

Hence, under f(0), there will be 3 functions called sequentially, f(0 + 1), f(0 + 2) and f(0 + 3), which are f(1), f(2) and f(3).

2nd Level

Now, let’s focus on the f(1) in the 2nd level.

In this function, num is valued as 1. Hence, the for loop in f(1) only loops twice, because for(int i = num; i < 3; i++) indicates that the loop starts from i = 1 to i = 2.

Hence, it will generate f(1 + 1) and f(1 + 2), which are f(2) and f(3).

3rd Level and Completed Graph

Following the pattern, the complete recursive function graph is a below. Note that it stops at f(3), which is because when num is 3, no forloop will be executed, thus no more recursive functions are called.

Execution Order

Now we have a complete diagram of the structure about the recursive functions called and it only left the order of executions.

This is the most Tricky part.

Some people may think that only when all the loops are executed in this level, can the code in the NEXT level can be excuted.

This is not correct.

The correct understanding is that, in the same level, 2nd loop will be executed ONLY when the 1st loop are completed, even if the 1st loop has recursive calls. That means, when all the recursive functions in the 1st loop must be completed, can the 2nd loop starts to execute.

The illustration is shown below. The function circled in green color can be executed only when all the functions circled in the red color all complete execution.

Therefore, the execution order of the functions can be determined as below.

Printing the Numbers

Finally, we can now determine how the numbers are printed.

At this stage, we must know WHAT number will be printed in the current function.

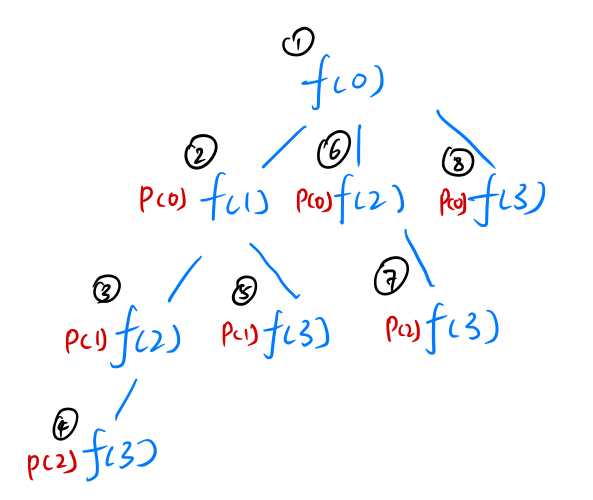
System.out.println(num); indicates that the variable num is printed. The value of num is passed from the parent function (which calls the current function). Hence, all the print function in the loop should print the same value.

In the following illustration, p() denotes System.out.println() function, and the value inside denotes the number to be printed.

Note that p() is shown at the left side of f(), it’s because p() is executed first and then f() is executed subsequently.

Hence, following the order of execution, we can get

Conclusion and Recommendation

The questions like this one are quite tricky as you need to identify the correct order of execution and correct value to be printed. Also, the dynamic start condition of for loops makes it more complicated when analysing.

After analysis of the problem, I summarised my thoughts and recommend a way of interpretation.

Identify which variable is controlling the depth of recursive functions. In this case, num is controlling the depth.
Identify which variable is controlling the loop count in a recursive functions. In this case, i is controlling the loop count, and you must note that all the loops in this function are at the same depth.
Understand that the second loop can only be executed after the first loop has been fully executed including all the recursive functions called in the first loop.
Draw the graph to help you analyse.